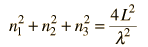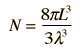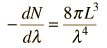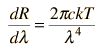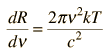- 佛網Life論壇 (http://buddhanet.idv.tw/aspboard/index.asp)
-- 奇文共賞版(Life論壇) (http://buddhanet.idv.tw/aspboard/list.asp?boardid=4)
---- 【轉貼】近代物理-黑體輻射(Blackbody Radiation) (http://buddhanet.idv.tw/aspboard/dispbbs.asp?boardid=4&id=72642)
-- 發表時間:2023/3/6 下午 12:13:56
-- 【轉貼】近代物理-黑體輻射(Blackbody Radiation)
Blackbody Radiation"Blackbody radiation" or "cavity radiation" refers to an object or system which absorbs all radiation incident upon it and re-radiates energy which is characteristic of this radiating system only, not dependent upon the type of radiation which is incident upon it. The radiated energy can be considered to be produced by standing wave or resonant modes of the cavity which is radiating.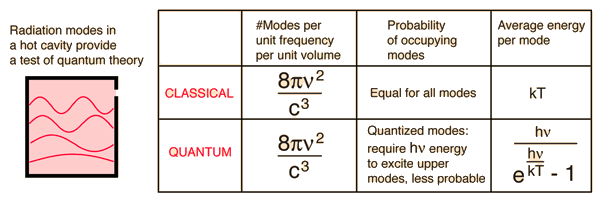
| Index Blackbody radiation concepts Great experiments of physics | ||||
| Go Back |
Cavity ModesA mode for an electromagnetic wave in a cavity must satisfy the condition of zero electric field at the wall. If the mode is of shorter wavelength, there are more ways you can fit it into the cavity to meet that condition. Careful analysis by Rayleigh and Jeans showed that the number of modes was proportional to the frequency squared. | Index Blackbody radiation concepts | ||
| Go Back |
Planck Radiation FormulaFrom the assumption that the electromagnetic modes in a cavity were quantized in energy with the quantum energy equal to Planck\'s constant times the frequency, Planck derived a radiation formula. The average energy per "mode" or "quantum" is the energy of the quantum times the probability that it will be occupied (the Einstein-Bose distribution function): 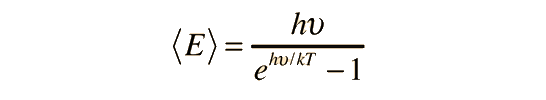 This average energy times the density of such states, expressed in terms of either frequency or wavelength 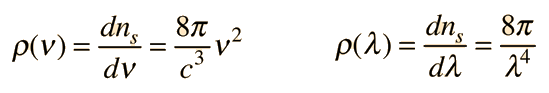 gives the energy density, the Planck radiation formula.
The Planck radiation formula is an example of the distribution of energy according to Bose-Einstein statistics. The above expressions are obtained by multiplying the density of states in terms of frequency or wavelength times the photon energy times the Bose-Einstein distribution function with normalization constant A=1. To find the radiated power per unit area from a surface at this temperature, multiply the energy density by c/4. The density above is for thermal equilibrium, so setting inward=outward gives a factor of 1/2 for the radiated power outward. Then one must average over all angles, which gives another factor of 1/2 for the angular dependence which is the square of the cosine.
| Index Blackbody radiation concepts | |||||
| Go Back |
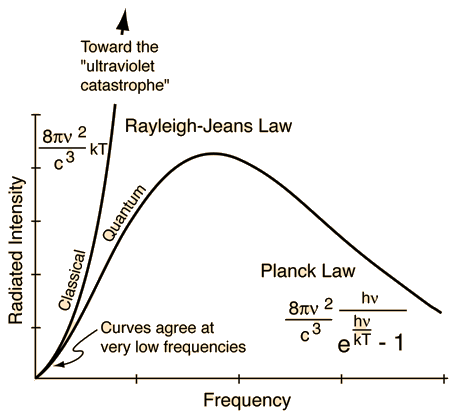
Rayleigh-Jeans vs PlanckComparison of the classical Rayleigh-Jeans Law and the quantum Planck radiation formula. Experiment confirms the Planck relationship.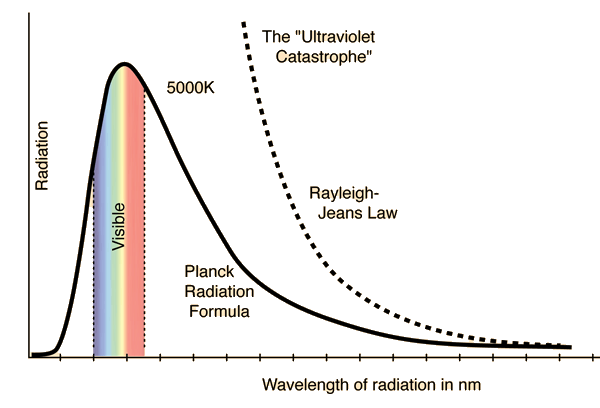 Comments on the development of the Rayleigh-Jeans Law
| Index Blackbody radiation concepts | |||
| Go Back |
Blackbody Intensity as a Function of Frequency
| Index Blackbody radiation concepts | ||||
| Go Back |
Comments on the Development of the Rayleigh-Jeans LawThe Rayleigh-Jeans Law was an important step in our understanding of the equilibrium radiation from a hot object, even though it turned out not to be an accurate description of nature. The careful work in developing the Rayleigh-Jeans law laid the foundation for the quantum understanding expressed in the Planck radiation formula. In outline form, here are the steps which led to the Rayleigh-Jeans law.
| Index Rayleigh- Jeans references Blackbody radiation concepts | ||||||||||||||||||||
| Go Back |