Angular Momentum of a Particle
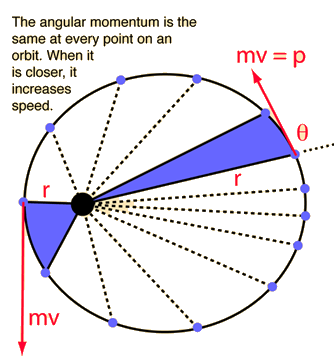 Angular MomentumThe angular momentum of a rigid object is defined as the product of the moment of inertia and the angular velocity. It is analogous to linear momentum and is subject to the fundamental constraints of the conservation of angular momentum principle if there is no external torque on the object. Angular momentum is a vector quantity. It is derivable from the expression for the angular momentum of a particle 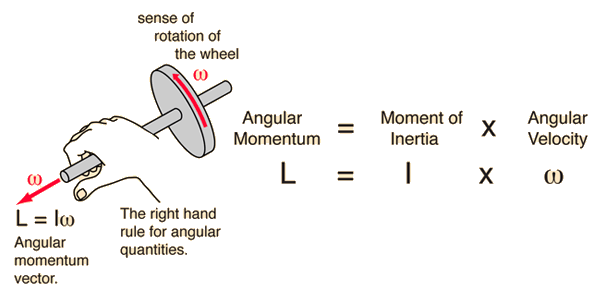 Angular and Linear MomentumAngular momentum and linear momentum are examples of the parallels between linear and rotational motion. They have the same form and are subject to the fundamental constraints of conservation laws, the conservation of momentum and the conservation of angular momentum . 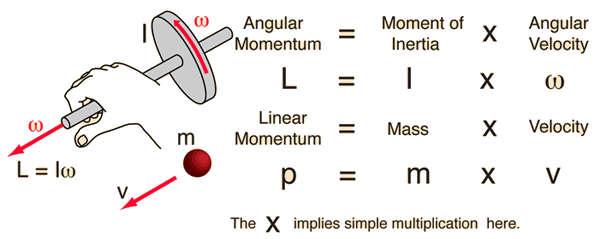 文章出處:https://reurl.cc/RvyglG | The angular momentum of a particle of mass m with respect to a chosen origin is given by or more formally by the vector product The direction is given by the right hand rule which would give L the direction out of the diagram. For an orbit, angular momentum is conserved, and this leads to one of Kepler's laws. For a circular orbit, L becomes |